Demystifying Deep Learning: Part 3
Learning Through Gradient Descent
August 03, 2018
5 min read
Having looked at linear and logistic regression, we will look at how these algorithms “learn”.
Loss Functions:
For a machine algorithm to learn, it needs some way of evaluating its performance. The loss function (aka cost function) is a function that quantifies the errors in its predictions - lower error is better. Thus, a way for the algorithm to improve is to minimise this loss function, which, if chosen correctly, will also result in the model learning. The algorithm can tweak its weights and biases to get the value of the loss function as low as possible. When thinking of the correct loss function to use, it helps to think about the problem we are trying to solve:
Intuition: For linear regression, we want to plot a straight line of best fit - i.e one that is as close to as many of the points as possible. So one good idea is to minimise the mean distance between the straight line and the points. In dimensions, we consider the distance between the point and the hyperplane - i.e. take the difference between the prediction (projection of the value onto the plane) and the actual value. We then square it (so it ensures the value is always positive), and then do this for all predictions and take the mean.
Maths: We denote the loss function as . Note the factor of is for convenience.
Code: As before we are continuing with the same motivating examples of housing prices for linear regression and breast cancer for logistic regression. You can access the full code in the accompanying Jupyter notebook.
def MSE_loss(Y, Y_pred):m = Y.shape[1]return (1.0/(2*m))*np.sum(np.square(Y_pred-Y))
Next, moving onto logistic regression:
Intuition: The aim with logistic regression is to maximise the probability of getting the correct label across all the examples.
Maths: Here, it is easier to present the intuition interspersed with the maths:
For a single example, we want:
This translates to finding that maximise the probability of getting the correct label given the value of , parameterised by . Since each training example is independent of each other, to get the total probability we multiply the probabilities together:
This could lead to underflow, when multiplying tiny probabilities together, so instead we take the log and maximise that. Since we now have:
If we recall our interpretation of the output of logistic regression, we have that:
Putting all these pieces together, it is time to look at the loss function for logistic regression:
Breaking it down:
First, we have a negative sign in front of the entire expression: this is because we want to maximise the log probability, but we can only minimise the loss function.
We divide the sum by - this corresponds to the “mean” probability, and since is the same for all it doesn’t affect our objective.
There are two terms in the summation: the first is and the second is . These combine to give since when only the second term contributes, and likewise when only the first term contributes, since the and terms set the other to zero respectively.
Code:
def log_loss(Y, Y_pred):m = Y.shape[1]return (-1.0/m)*np.sum(Y*np.log(Y_pred) + (1-Y)*np.log(1-Y_pred))
So now that we have defined our loss function, let’s look at how we minimise it:
Gradient Descent:
Intuition:
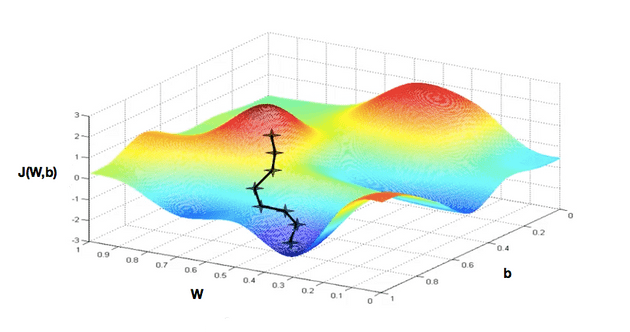
Think of the loss function as a surface with hills and valleys, and the current value of the loss for the algorithm as a point on this surface (see above image). We want to minimise it, so we want to keep taking steps down the slope of the surface into the valley.
The slope of the surface is the gradient at that point, and so we want to keep taking steps in the direction down the gradient to the minimum, where the gradient is 0. This is the gradient descent algorithm.
Maths:
The gradient descent update equation is as follows:
is the learning rate hyperparameter - this controls the size of the step we take each iteration. If is too large we may overshoot the minimum and diverge, whereas if is too small it will take too long to converge to the minimum.
Now it’s time to compute and .
When thinking about computing partial derivatives, it helps to have an intuitive understanding, to make sense of the maths expression that results, especially when we later try to take partial derivatives with respect to each value in a matrix.
Some ideas worth bearing in mind as we go into this calculation and more complicated expressions later on:
Partial Derivative Intuition: Think of loosely as quantifying how much would change if you gave the value of a little “nudge” at that point.
Breaking down computations - we can use the chain rule to aid us in our computation - rather than trying to compute the derivative in one fell swoop, we break up the computation into smaller intermediate steps.
Computing the chain rule - when thinking about which intermediate values to include in our chain rule expression, think about the immediate outputs of equations involving - which other values get directly affected when I slightly nudge ?
Let’s apply these ideas in the context of linear and logistic regression - the key here is not so much the equations themselves, but to build up this intuition, since we can boil down most of the more advanced networks with this same reasoning:
First, linear regression - we’ll break it down into two steps:
Let’s consider one particular prediction Intuitively, nudging it will only affect the squared error for that example and indeed taking the partial derivative:
(note the factor of in J has cancelled to leave .)
For this example let’s consider the effect of nudging a particular weight - intuitively since it is multiplied by in the calculation, the corresponding amount will move is times that nudge. And since the bias isn’t multiplied by anything, the nudge should be of the same magnitude. Indeed the maths reflects this:
Now we’ve looked at the partial derivative intuition, let’s look at computing the chain rule. If we nudge or intuitively we will affect all predictions, so therefore we need to sum across the examples . So we have that:
and:
Now we can move onto the case of logistic regression - we’ll introduce an intermediate step :
Again, nudging will only affect the error for that example :
The derivative of with respect to can be rearranged:
This is a neat result to remember:
Great, after that algebraic rearrangement, we have a nice result, so let’s compute chain rule - note a nudge in only affects so:
So we have, multiplying out:
If we compare with linear regression, it turns out that the equations for the partial derivatives for and are the same, since the equation for in logistic regression is the same as in linear regression.
We just have one final step to finish things off! Just like in the last post, we can rewrite the equation for as a matrix multiplication: note that is a 1 x n matrix, is a m x n matrix and is a 1 x m matrix. So:
The equation for the is the same, only that we use subscripts for the matrix instead of and ditto for .
So by breaking it down into many small steps, we have our final equations (for both linear and logistic regression):
Code:
def grads(X, Y, Y_pred):m = Y.shape[1]dW = (1.0/m)*np.dot(Y_pred-Y,X.T)db = (1.0/m)*np.sum((Y_pred-Y),axis=1,keepdims=True)return dW, dbdW, db = grads(X, Y, Y_pred)#gradient descent updateW = W - alpha*dWb = b - alpha*db
Conclusion:
With the last two posts, you have now coded up your first two machine learning algorithms, and trained them! Machine learning can be applied to diverse datasets - the motivating examples that you trained your algorithms - housing prices and breast cancer classification - being two great examples of that!
If you made it through the maths, you’ve understood the fundamentals of most learning algorithms - we’ll use this as building blocks for neural networks next.