Demystifying Deep Learning: Part 6

Optimising Learning

Improving Gradient Descent

Gradient descent is a good learning algorithm for neural networks, however we can do better to improve learning.

Different Optimisers and their performances

Stochastic / mini-batch gradient descent:

When we computed the forward and backprop steps for our neural network, we did so on the entire data set. However, as the networks get deeper, there are more matrix multiplications to be computed so this is very computationally expensive. Another factor is the size of the dataset, which for many tasks has 100,000+ examples.

So you might think that to speed things up we should only look at one example at a time rather than 100,000 and update the parameters with the gradient from that example. This is called stochastic gradient descent (SGD) where the term stochastic is because the gradient steps are noisy and appears random, since improving on one example may not necessarily improve performance over the entire training set, and the model may actually go in the a slightly different direction. However the idea is on average the model will go in the right direction, and by taking more frequent steps it will get there faster.

However stochastic gradient descent isn’t very efficient since we lose out on the benefit of computing multiple examples in parallel in the forward and backward steps. So while we make more steps, one epoch (cycle through the entire training set) is much slower.

So instead as a compromise between the frequency of steps and time for each epoch, we compute the gradient on a subset of the dataset each time. We call this subset a minibatch (with the whole dataset referred to as a batch) - giving the name mini-batch gradient descent. Since the network is learning from only that batch, the gradient is still noisy, but it is averaged over the batch so more stable than stochastic gradient descent.

One other benefit the noise has is that it means the network doesn’t fully converge to, and thus get stuck in, local minima - this means the network can actually find better local minima and thus perform better.

In practice, we almost always use minibatch gradient descent when training neural networks however confusingly it is commonly also referred to as SGD, despite being over multiple examples, not a single example.

Momentum

Great, so we’ve improved the speed of training but we still have the issue that the model “jumps around” a lot, due to the noisy gradient updates - this is where momentum comes in.

Intuition:

Consider a valley with steep sides - rather than bouncing around as with SGD we would like the model to keep going down the steep sides like a ball and pick up momentum. Momentum applies the same principle as the physics analogy - we would like to keep moving in the average direction of the recent gradient updates.

Maths:

The update equation is as follows (where $\beta$ is a hyperparameter and $\nabla x$ is a notational convenience for $\nabla_x J$ - the gradient with respect to x):

$v*t = \beta\*v*{t-1} + \nabla x_t$

$x*t = x*{t-1} - \alpha v_t$

Notice how we take a step using the overall momentum (rather than the gradient as in SGD). A typical value of $\beta=0.9$ (though sometimes at the start of learning we set $\beta=0.5$ while we “warm up”).

This update equation for $v_t$ is known as an exponentially-weighted moving average - to see this let’s expand the equation:

$v*t = \nabla x_t + \beta( \nabla x*{t-1} + \beta\*v\_{t-2})$

$v*t = \nabla x_t + \beta\nabla x*{t-1} + + \beta^2\nabla x*{t-2} + \beta^3 \nabla x*{t-3} + \beta^4\nabla x\_{t-4} ...$

The use of the term exponentially-weighted comes from the $\beta$ being raised to higher powers as we look at earlier iterations - since $\beta<1$ this means we weight the previous iterations less when taking our average.

Code:

One improvement we can make to momentum is to correct our gradient update to account for the momentum - using our physics analogy we look ahead to where the ball’s momentum would be taking it first, then compute our our gradient to compensate for this. This is called Nesterov Accelerated Gradient momentum.

So first we compute:

$\tilde{x}_{t-1} = x_{t-1} -\beta v\_{t-1}$

Then we compute $\nabla {\tilde{x}_{t-1}}$ with forward and backprop, and finally use the equation above for momentum but with $\nabla {\tilde{x}_{t-1}}$ as the gradient.

Momentum allows us to set a higher learning rate, because there will be fewer oscillations, since they get damped by our momentum term. However, we can still do better than a fixed learning rate.

Learning rate

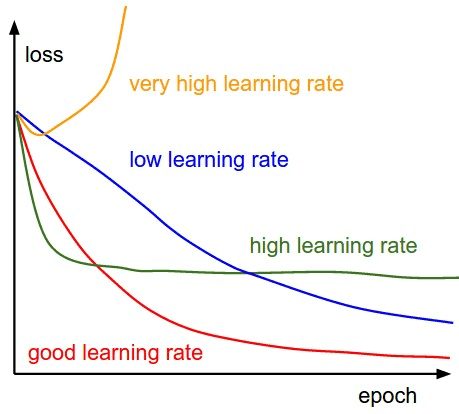
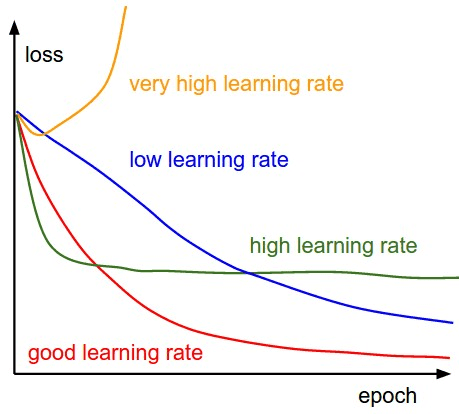
Recall in our Learning by Gradient Descent post we briefly touched upon the learning rate $\alpha$ and how it determines the size of the step we take - if it is too small learning is slow, whereas if it is too large we overshoot.

In the context of SGD the updates are noisy, so as we get towards the optimum value we want to take smaller and smaller steps to prevent us from overshooting once we are close. This is because the gradient at a minima (whilst zero when averaged across the entire training set) may not be exactly zero for just the minibatch, so smaller steps help aid convergence.

This idea of reducing the learning rate is known as learning rate decay. A simple way of reducing the learning rate may be in steps based on some heuristic e.g. halve it every 3 epochs (cycles through the training set). However, how do we choose this heuristic? These seem a bit arbitrary, and depends on the dataset.

We could use a mathematical equation instead to continually alter $\alpha$:

$\alpha = \alpha_0 e^{-kt}$ - exponential decay

$\alpha = \frac{\alpha_0}{1+kt}$ where (t = number of epochs).

This seems like a good solution but it poses another problem, which is that we now have two more hyperparameters - $\alpha_0$ and $k$ to add to the number of layers, number of units in each layer etc. This growing number of hyperparameters leads to more possibilities to search, which means we will have to train more models.

It turns out we can do even better.

Adaptive learning rates

We would like to have a finer control over the size of our weight updates - having one learning rate for all marginalises the rarely updated weights. One idea is to normalise our learning rate on a per-parameter basis - so more frequently updated parameters take smaller steps and infrequently updated parameters take larger steps.

Adagrad does this by considering the root-mean-square of the gradient updates - so (with $\epsilon=10^{-8}$ to prevent division by zero):

$x*t = x*{t-1} - \frac{\alpha}{\sqrt{\sum*{i=1}^{t-1} (\nabla x*{i})^2 + \epsilon}} \nabla x\_{t}$

One issue with this is that it is too aggressive and it reduces the learning rate too quickly. So we need a better way of getting an average of the gradient updates.

RMSProp takes Adagrad and instead of taking the sum of the squared gradients, takes the exponentially-weighted moving average, just like we did for momentum to get our average update, except here it is the average of the squared gradients ($\gamma=0.9$ is a good hyperparameter value).

$s*t = \gamma s*{t-1} + (1-\gamma)(\nabla x\_{t})^2$

$x*t = x*{t-1} - \frac{\alpha}{\sqrt{ s*t + \epsilon}} \nabla x*{t}$

Adam

This builds us up nicely to the Adam optimiser. We’ve looked at mini-batch gradient descent, discussed momentum and even talked about adaptive learning rates with RMSProp. What if we could combine all this?

One additional step in Adam is to introduce a bias correction term, to account for the fact that $s$ and $v$ are intially zero, so take time to warm up (for the first few timesteps they’ll be biased towards zero).

So the equations are:

For minibatch t:

$v*{t} = \beta_1 v*{t-1}+ (1-\beta*1)\nabla x*{t}$

$s*{t} = \beta_2 s*{t-1} + (1-\beta*2)(\nabla x*{t})^2$

$v*{t-corrected} = \frac{v*{t}}{1-\beta_1^t}$

$s*{t-corrected} = \frac{s*{t}}{1-\beta_2^t}$

$x*t = x*{t-1} - \alpha\frac{v*{t-corrected}}{\sqrt{s*{t-corrected}+\epsilon}}$

where $\beta_1=0.9$ , $\beta_2=0.999$ , $\epsilon = 10^{-8}$ (as recommended by the original Adam paper)

This is the most intuitive way of thinking about Adam. The name Adam comes from Adaptive Moment Estimation - $v$ is the first moment (mean) of the gradients and $s$ is the second moment (variance).

In practice we use Adam as the default optimiser for most neural networks, though in some cases SGD with Nesterov momentum has been shown to converge to a better final solution, though it may take far longer to do so.

Wrapping up

There are a lot of different optimisers out there, AdaDelta, Nadam, AdaMax and AMSGrad being a few that we haven’t covered.

After this post, you know how to get the model to train even better, using faster optimisation algorithms than the vanilla gradient descent algorithm we used in the previous posts.