Demystifying Deep Learning: Part 11
Backpropagation through, well, anything!
September 17, 2018
5 min read
Introduction
So far in this series, we have looked at the general principle of gradient descent, and how we computed backpropagation for each layer in a feedforward neural network, then generalising to look at backprop in different types of layers in a CNN.
Now we will take a step back and look at backpropagation in a more general sense - through a computation graph. Through this we’ll get a general intuition for how the frameworks compute their
We’ll use the LSTM cell as our motivating example - to continue the task of sentiment analysis on the IMDB review dataset - you can find the code in the accompanying Jupyter notebook
General Backpropagation Principles
Let’s look back at the principles we’ve used in this series:
Partial Derivative Intuition: Think of loosely as quantifying how much would change if you gave the value of a little “nudge” at that point.
Breaking down computations - we can use the chain rule to aid us in our computation - rather than trying to compute the derivative in one fell swoop, we break up the computation into smaller intermediate steps.
Computing the chain rule - when thinking about which intermediate values to include in our chain rule expression, think about the immediate outputs of equations involving - which other values get directly affected when we slightly nudge ?
One element at a time - rather than worrying about the entire matrix , we’ll instead look at an element . One equation we will refer to time and time again is:
A useful tip when trying to go from one element to a matrix is to look for summations over repeated indices (here it was k) - this suggests a matrix multiplication.
Another useful equation is the element-wise product of two matrices:
Sanity check the dimensions - check the dimensions of the matrices all match (the derivative matrix should have same dimensions as the original matrix, and all matrices being multiplied together should have dimensions that align.
A computation graph allows us to clearly break down the computations, as well as see the immediate outputs when computing our chain rule.
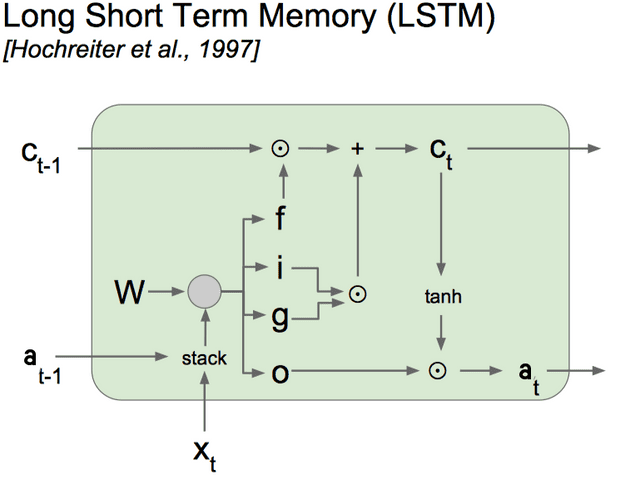
We will use the computation graph representation (shown above) of the LSTM to compute the gradients using backpropagation through time.
The LSTM Computation Graph
Forward Propagation equations
From the previous post, the forward propagation equations for one timestep in the LSTM are:
Notation used:
denotes a concatenation of the two matrices to form a x matrix. denotes matrix multiplication of and , whereas denotes elementwise multiplication. refers to the gate - see the previous post defining the LSTM for a full breakdown of the notation used.
To backpropagate through the cell, given the gradient with respect to and from the backprop from the next step, we need to compute the gradients for each of the weights and biases , and finally we will need to backpropagate to the previous timestep and compute the gradient with respect to and .
These are a lot of partial derivatives to compute - indeed as our neural networks get more complicated there will be more partial derivatives to calculate.
How can we use our computation graph to break this down?
Firstly, since the gate equations are identical, we can combine them so instead we have a x matrix containing the 3 gates’ outputs, and we can refer to the first third of the matrix and the other two thirds and respectively. Then we have one x matrix of weights for the gates and one x bias vector .
Next, we want to document all intermediate stages in calculation (every node in the graph).
So, walking through the computation graph node-by-node in the forward step:
We concatenate and to form the x concatenated input matrix .
We calculate the weighted input matrix for the gates using the weights and bias .
Likewise we calculate the weighted input for the candidate memory using the weight matrix and bias .
(NB: the diagram uses one weight matrix W, but it helps to think about these weights separately because of the different activation functions used)
We apply the sigmoid activation function to to get the Gate matrix (denoted by f, i, o in diagram), and the tanh activation function to to get (denoted by g in the diagram).
Since elementwise multiplication and addition are straightforward operations, for brevity we won’t give the intermediate outputs and their own symbols.
Let us denote the intermediate output as .
Now we have broken down the computation graph into steps, and added our intermediate variables we have the equations:
These equations correspond to the nodes in the graph - the left-hand-side variable is the ouput edge of the node, and the right-hand-side variables are the input edges to the node.
Backpropagation in a Computation Graph:
These equations allow us to clearly see the immediate outputs with respect to a variable when computing the chain rule - e.g. for the immediate outputs are and .
If we look at the equations / computation graph, we can more generally look at the type of operations, and then use the same identities:
Addition: If then and
Elementwise multiplication: If then and
tanh: If then
sigmoid: If then
Weighted Input: this is the same equation as the feedforward neural network. If then:
Armed with these general computation graph principles, we can apply chain rule. We elementwise multiply () the partial derivatives, i.e.
Also note we sum partial derivatives coming from each of the immediate outputs:
So if and , i.e. and are immediate outputs of in the computation graph, then we sum the partial derivatives:
In a deep learning framework like TensorFlow or Keras, there will be identities like this for each of the differentiable operations.
Backpropagation Through Time in an LSTM Cell
When trying to compute , we’ll use the general equation:
For brevity, we’ll substitute the value of using the operations’ identities above.
The equations are thus as follows:
From equation 7:
Using equation 6, and writing equation 5 as an equation for instead of (i.e. adding 1 to the timestep):
\frac{\partial{J}}{\partial{c^{< t>}}} = \frac{\partial{J}}{\partial{c^{< t+1>}}}_\Gamma_f + \frac{\partial{J}}{\partial{\tilde{a}^{< t>}}} _(1-\tilde{a}^{< t>2})
Also using equation 5:
From equations 3 and 4 respectively:
Equations 1 and 2 are identical, and so are the partial derivatives, differing only in subscript.
So by breaking the computation graph into many steps, we can break down the calculation into smaller simpler steps that just use the operations’ derivative identities mentioned above.
Code:
The motivating example we’ve looked at uses an LSTM network for sentiment analysis on a dataset of IMDB reviews
def backward_step(dA_next, dC_next,cache,parameters):(a_next, c_next, input_concat, c_prev, c_candidate,IFO_gates) = cachen_a, m = a_next.shapedC_next += dA_next* (IFO_gates[2*n_a:]*(1-np.tanh(c_next)**2))#we compute dC< t> in two backward steps since we need both dC< t+1> and dA< t>dC_prev = dC_next * IFO_gates[n_a:2*n_a]dC_candidate = dC_next * IFO_gates[:n_a]#derivative with respect to the output of the IFO gates - abuse of notation to call it dIFOdIFO_gates = np.zeros_like(IFO_gates)dIFO_gates[:n_a] = dC_next * c_candidatedIFO_gates[n_a:2*n_a]= dC_next * c_prevdIFO_gates[2*n_a:] = dA_next * np.tanh(c_next)#derivative with respect to the unactivated output of the gate (before the sigmoid is applied)dZ_gate = dIFO_gates* (IFO_gates*(1-IFO_gates))dA_prev = (parameters["Wg"].T).dot(dZ_gate)[:n_a]dWg = (1/m)*dZ_gate.dot(input_concat.T)dbg = (1/m)*np.sum(dZ_gate,axis=1, keepdims=True)dZ_c = dC_candidate * (1-c_candidate**2)dA_prev += (parameters["Wc"].T).dot(dZ_c)[:n_a]dWc = (1/m)*dZ_c.dot(input_concat.T)dbc = (1/m)*np.sum(dZ_c,axis=1, keepdims=True)return dA_prev, dC_prev, dWg, dbg, dWc, dbc
Practical Considerations:
When checking the equations for the backprop, it helps to have a numerical checker - I’ve written one in the accompanying Jupyter notebook.
Conclusion
This seems like a good juncture to recap the series so far.
We started the series looking at the most commonly used termninology, followed by looking at simple machine learning algorithms in linear and logistic regression, building up the intuition behind the maths behind gradient descent as we built up to a feedforward neural network.
Next we looked at the learning process itself, and how we could improve gradient descent itself, as well as debug our model to see whether it was learning or not.
Finally, we moved onto more specialised neural networks - CNNs and recurrent neural nets, not only looking at their theory but the motivation behind them. We also looked at the maths behind them, deriving the CNN backprop equations from scratch.
Now that we’re at the point that we’re able to understand backprop in a general computation graph, we can use the abstractions of the deep learning frameworks in subsequent posts.